Úplná množina operací symetrie se označuje jako grupa operací, což
je neprázdná množina G na níž je definována binární algebraická operace
(*), tzv. grupová operace. Množinu G nazveme grupou, jsou-li splněny tyto
postuláty:
Ke
každé uspořádané dvojici A, B ÎG
je přiřazen jednoznačně prvek CÎG,
psáno jako A*B = C
Pro
každé A,B,C Î
G platí: A*(B*C) = (A*B)*C
Existuje
takový prvek E Î G, že platí: A*E = E*A = A, kde A je libovolný prvek grupy G
Ke
každému prvku A Î G existuje A-1 Î
G takový, že A*A-1=
A-1*A = E
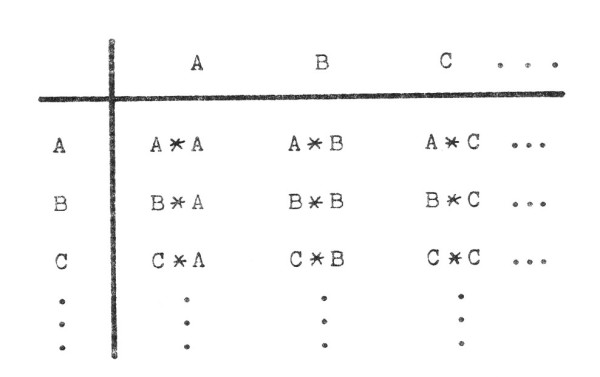
Operace symetrie jsou prvky grupy operací. Výsledky aplikace grupové operace (*) „násobení“ mezi všemi dvojicemi prvků konečné grupy G = {A, B, C, …} zapisujeme do formy multiplikační tabulky (viz obrázek).
