Odvození transformačních matic pro různé typy rotace

Je dán bod P [x,y,z] v ortogonální soustavě souřadnic. Odvoďme transformační rovnice pro souřadnice (x´, y´, z´) tohoto bodu v transformované soustavě, která vznikne otočením o úhel a kolem osy z v kladném smyslu (proti směru hodinových ručiček). Otočení souřadné soustavy o daný úhel dává stejný výsledek jako otáčení bodu P o stejný úhel podle středu souřadné soustavy.

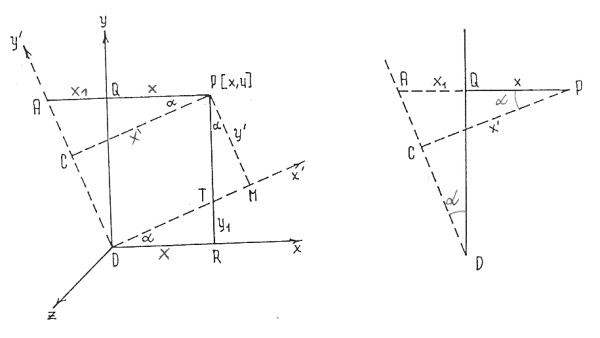
Situace je na obrázku (Kühn, Weiss 1978) a z trojúhelníku ACP můžeme vyjádřit:
x´= (x₁ + x) cos a
a z trojúhelníku DQA pak plyne:
x₁= y tg a
což po dosazení znamená
x´= x cos a + y sin a.

Obdobně plyne i z trojúhelníků TMP a DQA:
y´= (y - y₁) cos a a y₁ = x tg a.

Po dosazení
y´= -x sina + y cosa.

Soustava transformačních rovnic bude mít tento tvar:
x´ = x cosa + y sina
y´ = -x sina + y cosa
z´ = z

V maticovém tvaru bude transformace vyjádřena:

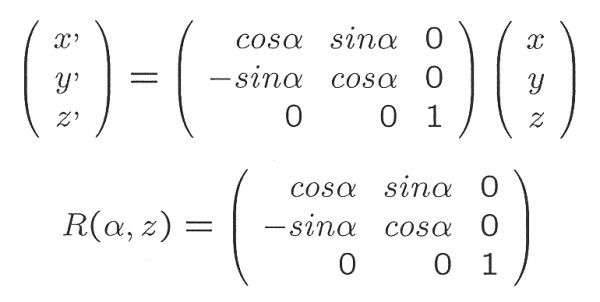
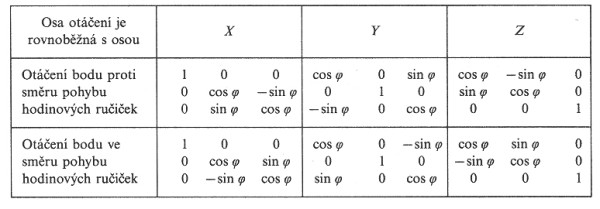
Tabulka transformačních matic pro obecný úhel pro jednotlivé osy x, y, z (podle Krause, 1993).