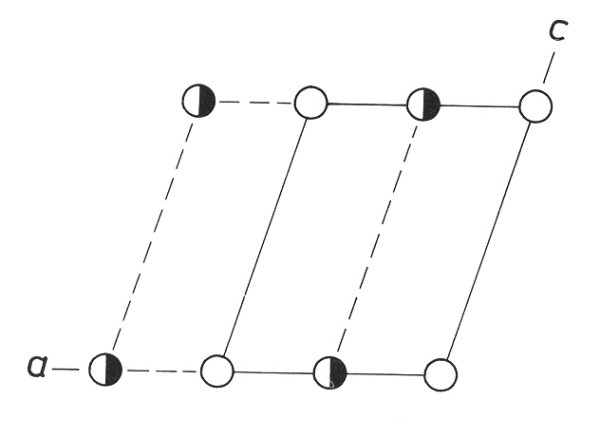
Do monoklinické P-mřížky vložíme další mřížkovou rovinu s mřížkovým bodem v ½,½,0. Nový mřížkový bod centruje plochu a, b základní buňky. Mluvíme o bazálně centrované C-mřížce nebo jednoduše o C-mřížce.

Do monoklinické P-mřížky vložíme další mřížkovou rovinu s mřížkovým bodem v 0, ½,½. Pokud bod nové roviny centruje plochu (b, c), bude výsledkem bazálně centrovaná A-mřížka. Jelikož v monoklinické soustavě mohou směry a i c ležet kdekoliv v rovině zrcadlení, mohou být zaměněny a A-mřížka se konvertuje na C-mřížku.
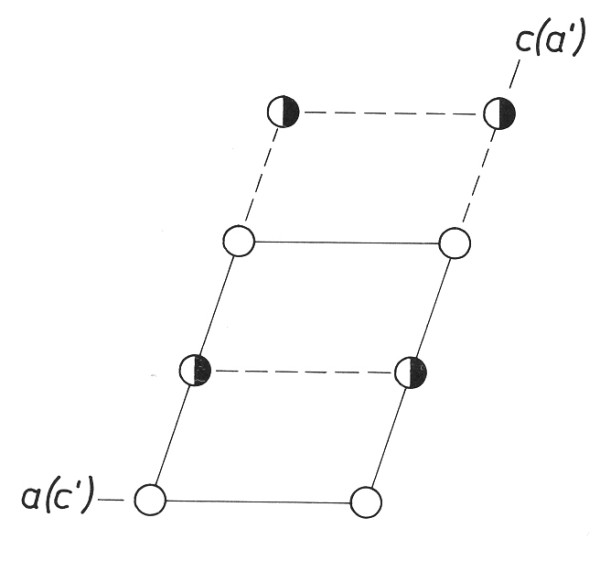
Do
monoklinické P-mřížky vložíme další mřížkovou rovinu s mřížkovým
bodem v ½,0,½. Výsledkem je bazálně centrovaná B-mřížka, ze
které lze vhodným výběrem udělat menší primitivní základní buňku s monoklinickou
symetrií.
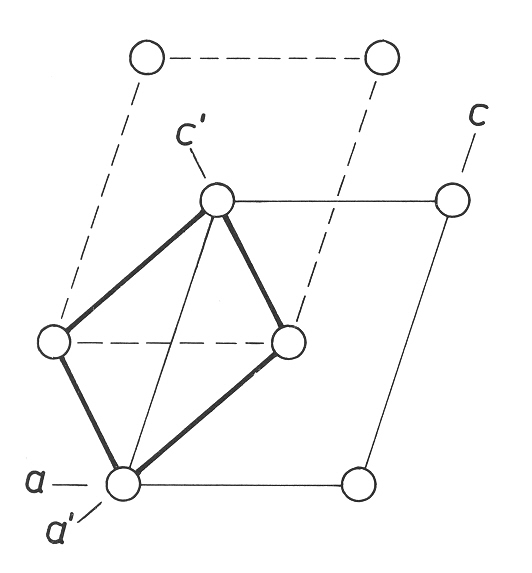
Do
monoklinické P-mřížky vložíme další mřížkovou rovinu s mřížkovým
bodem v ½,½,½. Vznikne tělesově centrovaná základní buňka,
krátce I-mřížka. Podobně jako u A-mřížky ji lze vhodným výběrem souřadnic
konvertovat na monoklinickou C-mřížku.
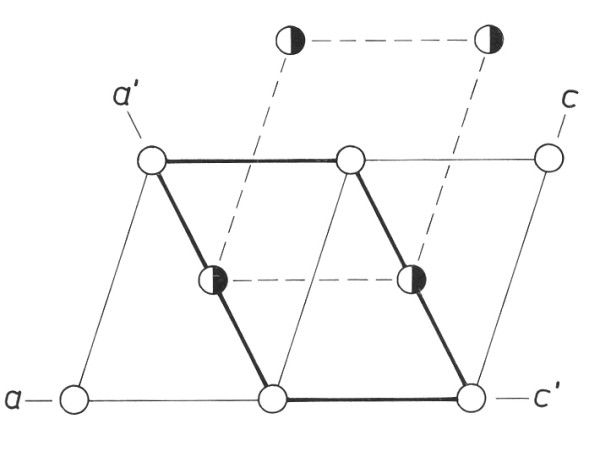
Do
monoklinické P-mřížky vložíme další mřížkovou rovinu s mřížkovými
body v ½,0,0; 0,½,0 nebo 0,0,½. Ve všech případech je výsledkem
prosté rozpůlení základní buňky a nevznikne žádný nový typ buňky.
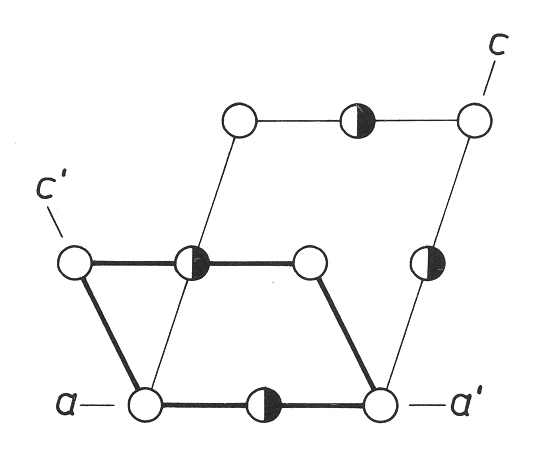
Je
také možné vložit dvě mřížkové roviny současně, např. jako u C- a
A-mřížky. Přibudou nám mřížkové body v ½,½,0 a 0,
½,½. Jelikož je nezbytné, aby všechny mřížkové body měli
stejné okolí a rovnoběžné mřížkové přímky stejnou periodu identity,
musí být přidán další mřížkový bod do ½,0, ½. Tím jsou
všechny plochy buňky centrované a jedná se o plošně centrovanou F-mřížku.
Monoklinickou F-mřížku lze redukovat na C-mřížku s polovičním
objemem.
Jak je vidět z textu výše, v rámci monoklinických centrovaných mřížek lze redukovat A,I,F-mřížky na C-mřížku a B-mřížku na P-mřížku.
Obrázky v textu podle Borchardt-Ott (1995).