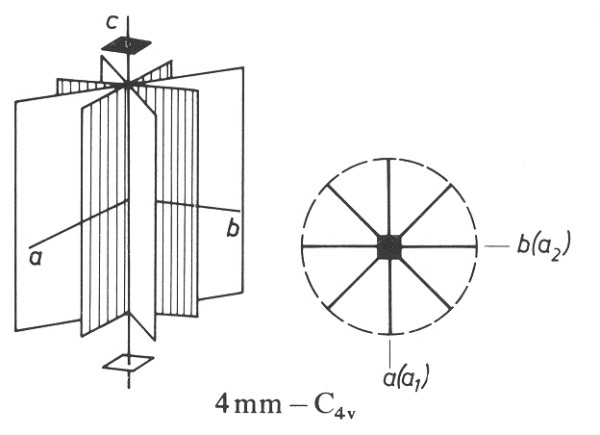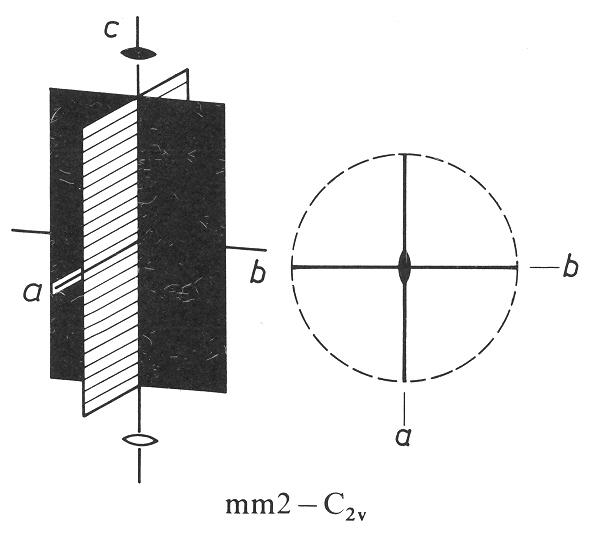
Obrázek 15-2. V průniku n rovin symetrie existuje n-četná rotační osa symetrie, jejíž četnost závisí na úhlu (n = p/a), který svírají protínající se roviny symetrie. Na horním obrázku se kolmo protínají dvě roviny symetrie a vzniká dvojčetná rotační osy symetrie, na spodním obrázku se protínají čtyři roviny po 45° a v jejich průsečíku vzniká čtyřčetná rotační osy symetrie. Podle Borchardt-Ott (1995).