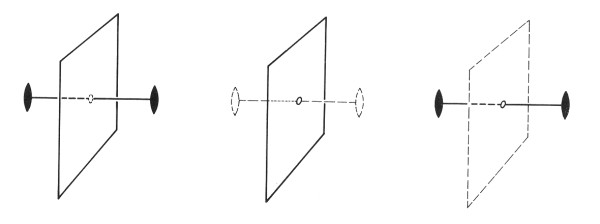
Obrázek 15-4. Rotační osy symetrie sudého řádu (2, 4, 6) sdružené s kolmou rovinou symetrie podmiňují přítomnost středu symetrie. Zde příklad kombinace dvojčetné rotační osy symetrie a kolmé roviny symetrie: máme-li osu a rovinu, odvodíme střed; ze středu a roviny odvodíme osu; ze středu a osy odvodíme rovinu. Podle Borchardt-Ott (1995).
