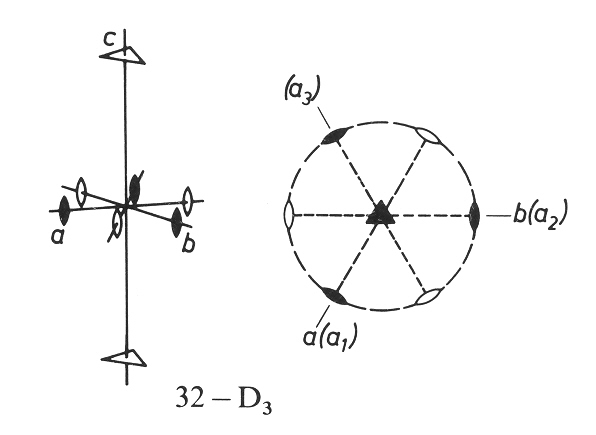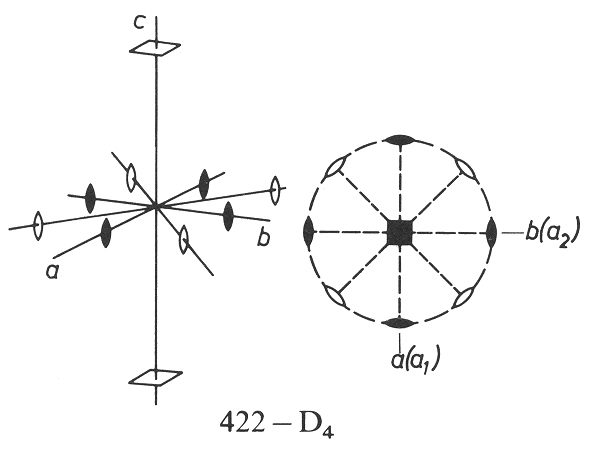
Obrázek 15-5. Nalezneme-li v celkové symetrii dvě dvojčetné rotační osy symetrie svírající úhel a, existuje na ně kolmá n-četná rotační osa symetrie, kde n = p/a a počet dvojčetných rotačních os symetrie se doplní na n. Na horním obrázku je příklad čtyřčetné rotační osy symetrie a na ni jsou kolmé čtyři dvojčetné osy, které svírají úhel 45°. Na spodním obrázku je vertikálou trojčetná rotační osa symetrie a na ni jsou kolmé tři dvojčetné osy, svírající úhel 60°. Podle Borchardt-Ott (1995).