Izogonální prostorové grupy

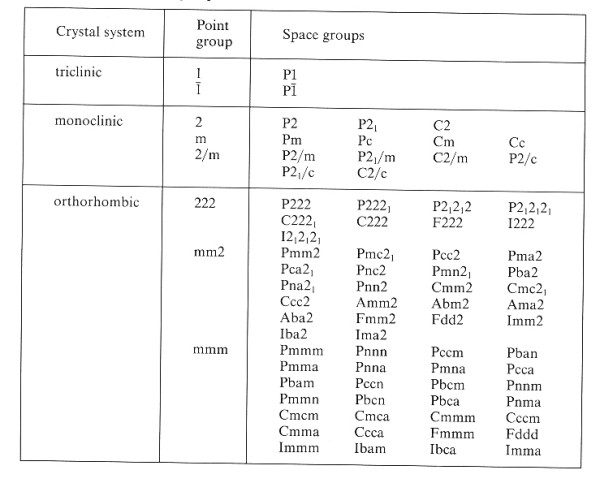
Izogonální prostorové grupy jsou takové, které byly odvozeny od stejné bodové grupy a zachovávají úhlové vztahy mezi operacemi symetrie výchozí bodové grupy.

Na obrázku jsou rozděleny všechny prostorové grupy podle soustav a bodových grup.

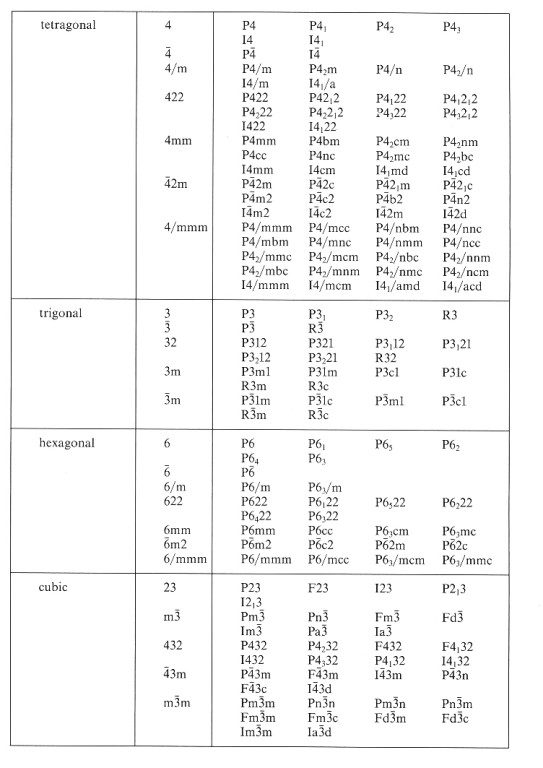
Chceme-li z prostorové grupy získat odpovídající bodovou grupu, musíme redukovat všechny prvky obsahující translaci na beztranslační podle schématu:

• 2₁ na 2

• 3₁, 3₂ na 3

• 4₁, 4₂, 4₃ na 4

• 6₁, 6₂, 6₃, 6₄, 6₅ na 6

• a, b, c, n, d (skluzové roviny) na m (rovina symetrie)

Příklad: Máme-li prostorovou grupu 4₁/m 2/n 2/n, převedeme všechny prvky symetrie obsahující translaci na beztranslační a dostaneme bodovou grupu 4/m 2/m 2/m.