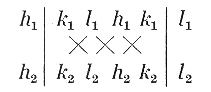
Pásmo
je soubor ploch, které mají hrany navzájem rovnoběžné a zároveň jsou
rovnoběžné s osou pásma, která prochází středem krystalu. Obecně
se osa pásma označuje jako [uvw], což může chápat jako symbol libovolného
bodu, který leží na ose pásma jinde než v počátku.
Libovolná
plocha patřící do pásma bude značena (hkl). Posunutím této plochy do počátku
souřadnic, bude osa pásma ležet v rovině (hkl) a libovolný bod [uvw]
bude ležet v této rovině. Potom bude platit rovnice:
hu
+ kv + lw = 0 (pásmová rovnice)
Jelikož
pásmo a jeho osa jsou jednoznačně určeny dvěma různoběžnými plochami pásma,
lze z Millerových indexů těchto ploch (h1k1l1)
a (h2k2l2) vypočítat symbol osy pásma [uvw]. Protože osa pásma leží v obou
plochách platí:
h1u + k1v + l1w
= 0
h2u + k2v + l2w
= 0
Ze dvou rovnic dokážeme vypočítat poměr u : v : w pomocí následujícího vztahu:
u : v : w = (k1l2 - k2l1) : (l1h2 - l2h1) : (h1k2 - h2k1).
Přehlednější je však vyjádření pomocí determinačního schématu:
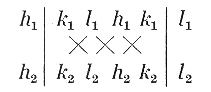
Zcela obdobný je i výpočet symbolu plochy společné dvěma pásmům, máme-li symboly os obou pásem.
Příklad 1. Určete osu pásma z ploch (110) a (010).
Dosadíme do výše uvedených vztahů:
u = 1∙0 - 0∙1 = 0
v = 0∙0 - 1∙0 = 0
w = 1∙1 - 1∙0 = 1
Nebo determinační schéma:
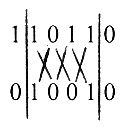
Osa zóny je [001].
Příklad 2. Zjistěte, zda krystalové plochy (210) a (211)
leží v pásmu [001].
Leží-li plocha v určitém pásmu, musí být splněna pásmová rovnice
a tak stačí dosadit:
pro (210): 2∙0 + 1∙0 + 0∙1 = 0
pro (211): 2∙0 + 1∙0 + 1∙1 = 1
Výsledek druhé rovnice není nulový a proto tato plocha v pásmu [001] neleží.