Vycházíme z principů stereografické projekce. Projekční rovinou je kruh (průnik s pomyslnou projekční koulí v rovníku). Čerchovaně nebo slabě je zakreslen obrys kruhu a předozadní a pravolevá souřadná osa, vertikála je kolmá na nákresnu v bodě křížení os a, b (střed kruhu). Do tohoto obrazce zaneseme symboly prvků symetrie – značka pro osy různé četnosti a silnou čarou roviny symetrie.

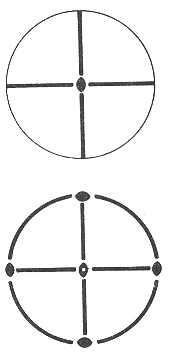
Příklad 1. Vyjádření symetrie bodové grupy pomocí stereogramu. Horní stereogram obsahuje dvě vertikální roviny symetrie a v jejich průsečíku se nachází dvojčetná rotační osa symetrie. Jedná se o symetrii mm2, oddělení rombicky pyramidální. Spodní stereogram obsahuje tři roviny symetrie a na ně kolmé tři dvojčetné rotační osy symetrie v osních směrech. Symetrie je 2/m 2/m 2/m, oddělení rombicky dipyramidální.
Příklad 2. Vyjádření vztahu mezi prvky symetrie a krystalovými plochami na krystalu.
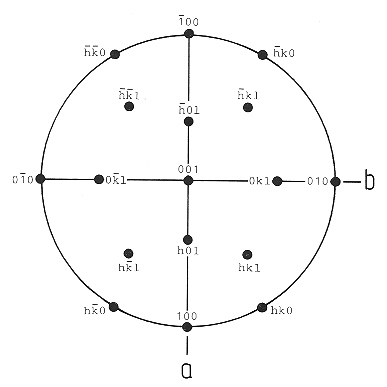
Na stereogramu oddělení rombické soustavy 2/m 2/m 2/m jsou zakresleny projekční body všech krystalových tvarů (pouze horní polovina krystalu). Plochy (hkl), (-hkl), (-h-kl) a (h-kl) jsou v obecné poloze a tvoří horní polovinu rombické dipyramidy. Plochy typu (hk0), (h0k) a (0kl) leží na rovině symetrie a představují dvojúseková prizmata. Plochy typu (100), (010) a (001) leží na rovině symetrie a dvojčetné rotační ose symetrie a reprezentují jednoúsekové pinakoidy.