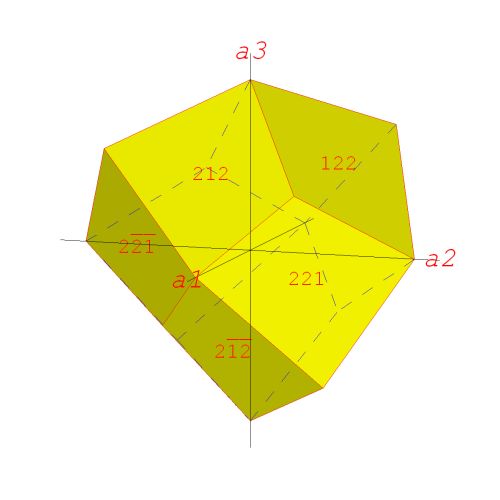
Krystalový tvar
Krystalový tvar se skládá ze skupiny krystalových ploch, které mají stejný vztah k prvkům symetrie a stejné chemické a fyzikální vlastnosti. Aplikujeme-li na zvolenou krystalovou plochu operace symetrie příslušné bodové grupy, získáme určitý počet stejnocenných krystalových ploch. Soubor ekvivalentních krystalových ploch se nazývá krystalový tvar. Krystalový tvar je definován indexem jedné z ploch krystalového tvaru. Pro označení tvaru se používá Millerových symbolů ve složených závorkách {hkl}.

Příklad krystalového tvaru tetragon-trioktaedru v kubické soustavě.
Přehled uvádí všechny krystalové tvary s počtem jejich ploch.
|
č. |
Jméno
podle Groth-Rogerse |
poč. ploch |
|
1 |
pedion |
1 |
|
2 |
pinakoid |
2 |
|
3 |
dóma |
2 |
|
4 |
sfenoid |
2 |
|
5 |
rombické prizma |
4 |
|
6 |
trigonální prizma |
3 |
|
7 |
ditrigonální prizma |
6 |
|
8 |
tetragonální prizma |
4 |
|
9 |
ditetragonální prizma |
8 |
|
10 |
hexagonální prizma |
6 |
|
11 |
dihexagonální prizma |
12 |
|
12 |
rombická pyramida |
4 |
|
13 |
trigonální pyramida |
3 |
|
14 |
ditrigonální pyramida |
6 |
|
15 |
tetragonální pyramida |
4 |
|
16 |
ditetragonální pyramida |
8 |
|
17 |
hexagonální pyramida |
6 |
|
18 |
dihexagonální pyramida |
12 |
|
19 |
rombické dipyramida |
8 |
|
20 |
trigonální dipyramida |
6 |
|
21 |
ditrigonální dipyramida |
12 |
|
22 |
tetragonální dipyramida |
8 |
|
23 |
ditetragonální dipyramida |
16 |
|
24 |
hexagonální dipyramida |
12 |
|
25 |
dihexagonální dipyramida |
24 |
|
26 |
trigonální trapezoedr |
6 |
|
27 |
tetragonální trapezoedr |
8 |
|
28 |
hexagonální trapezoedr |
12 |
|
29 |
tetragonální skalenoedr |
8 |
|
30 |
hexagonální skalenoedr |
12 |
|
31 |
romboedr |
6 |
|
32 |
rombický disfenoid |
4 |
|
33 |
tetragonální disfenoid |
4 |
|
34 |
krychle (hexaedr) |
6 |
|
35 |
oktaedr |
8 |
|
36 |
rombický dodekaedr |
12 |
|
37 |
tetrahexaedr |
24 |
|
38 |
tetragon-trioktaedr |
24 |
|
39 |
trigon-trioktaedr |
24 |
|
40 |
hexaoktaedr |
48 |
|
41 |
tetraedr |
4 |
|
42 |
trigon-tritetraedr |
12 |
|
43 |
tetragon-tritetraedr |
12 |
|
44 |
hexatetraedr |
24 |
|
45 |
pentagon-trioktaedr |
24 |
|
46 |
dihexaedr |
12 |
|
47 |
didokaedr |
24 |
|
48 |
pentagon-tritetraedr |
12 |