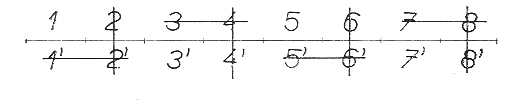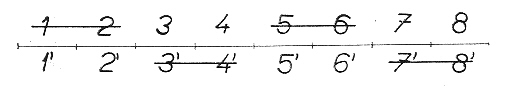
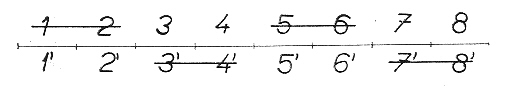
Odvozování krystalových tvarů meroedrickou operací
Všech 32 bodových grup (krystalových oddělení) můžeme rozdělit do sedmi krystalových soustav. V každé soustavě existuje právě jedno oddělení, které má maximální možnou symetrii. V trojklonné soustavě je to oddělení pinakoidální, v monoklinické soustavě oddělení prizmatické, v rombické soustavě oddělení dipyramidální, v tetragonální soustavě oddělení ditetragonálně dipyramidální, v hexagonální soustavě oddělení dihexagonálně dipyramidální, v trigonální soustavě oddělení ditrigonálně skalenoedrické a konečně v kubické soustavě oddělení hexaoktaedrické. Všechna uvedená oddělení jsou pojmenována podle krystalových tvarů, které mají v dané soustavě maximální počet ploch. Takové tvary se označují jako holoedry (plnotvary) a jejich oddělení jsou holoedrická (plnoplochá).
Další krystalové tvary všech oddělení, můžeme odvodit z holoedrických tvarů meroedrickou operací (částečnou redukcí) krystalových ploch. Pokud snížíme počet krystalových ploch holoedru na polovinu, dostaneme hemiedr (polotvar) a odpovídající krystalová oddělení budou hemiedrická. Při redukci ploch holoedru na čtvrtinu, dostaneme tetartoedr (čtvrtitvar) a odpovídající oddělení jsou tetartoedrická (čtvrtiplochá).
Hemiedrické tvary lze odvodit třemi typy meroedrických operací:
1. Hemiedrie skalenoedrického typu
Hemiedr skalenoedrického typu vznikne z holoedru {hkl} vynecháváním dvojic ploch střídavě nad horními a dolními oktanty resp. dodekanty. Hemiedr se formuje rozšířením nových ploch a protnutím v nových hranách. Skalenoedrická meroedrická operace může vést k pozitivnímu hemiedru, kdy se zachovají plochy v pozitivním oktantu, plochy 1, 2 vytínají kladnou část vertikály. Negativní hemiedr vznikne ze zachovaných ploch 1´,2´, které vytínají negativní část vertikály. Oba typy hemiedru jsou kongruentní, takže je můžeme navzájem převádět pouhým otočením kolem vertikály.
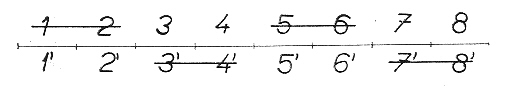
2. Hemiedrie trapezoedrického typu
Hemiedr trapezoedrického typu vzniká, když střídavě vynecháváme po jedné ploše v horní a dolní části holoedru {hkl}. Pokud zachováme v pozitivním oktantu pravou plochu 2, získáme hemiedr pravý, pokud ponecháme v novém tvaru levou plochu 1 (redukujeme plochu 2), získáme hemiedr levý. Oba tvary jsou vzájemně enantiomorfní a nelze jeden do druhého převést otočením okolo vertikály.
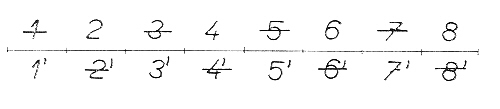
3. Hemiedrie dipyramidálního typu
Hemiedr dipyramidálního typu odvodíme střídavým vynecháváním vždy horního a dolního páru ploch holoedru. Při dipyramidální meroedrické operaci obdržíme opět pravý nebo levý hemiedr podle toho, z kterého oktantu, resp. dodekantu začneme s redukcí ploch. Oba hemiedry jsou kongruentní a lze je navzájem převést otočením kolem vertikální osy.
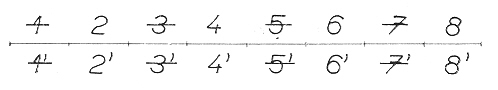
Tetartoedrické odvození tvarů se provádí uplatněním dvou meroedrických operací popsaných u hemiedrie. Příkladem může být kombinace skalenoedrické a dipyramidální meroedrie. Výsledkem je disfenická tetartoedrie, kdy vznikají čtyři tetartoedry: pozitivní a negativní pravý a pozitivní a negativní levý.