2.4. Přehled stereogramů (Gadolinova projekce) všech krystalografických oddělení (bodových grup)

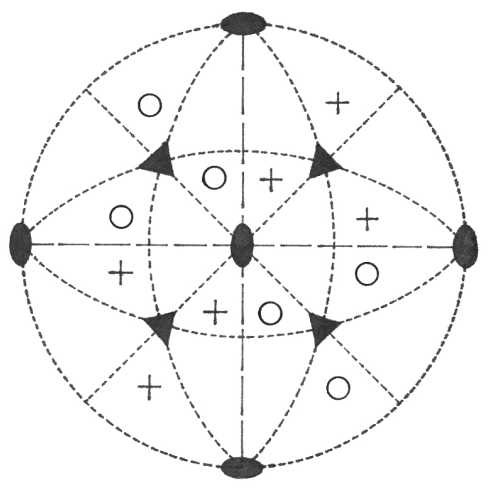
Pasná rovina krystalu je rovinou nákresny, vertikála c je tedy kolmá na nákresnu. V pravolevém směru je osa b (resp. a₂), v předozadním směru leží osa a. Plochy v horní polovině krystalu (nad plochou nákresny) jsou označeny křížkem, plochy ve spodní polovině krystalu (pod nákresnou) jsou označeny kroužkem. Je-li křížek umístěn v kroužku, leží plochy krystalu vzhledem k pasné rovině nad sebou. Značení prvků symetrie je provedeno pomocí obecně používaných symbolů.

Soustava triklincká

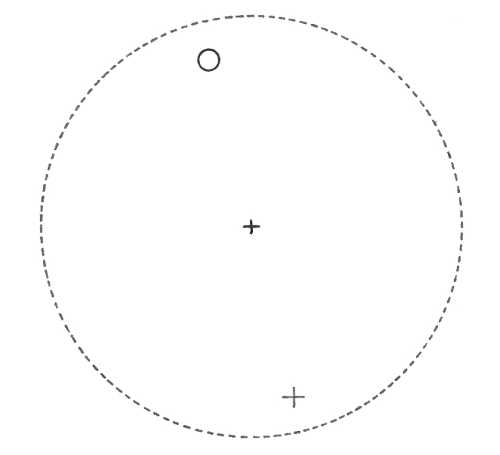
Oddělení triklinicky pinakoidální (-1) – přítomen je pouze střed symetrie, plocha v obecné poloze se zobrazí na druhou plochu a vznikne pinakoid - soubor dvou rovnoběžných ploch, symetrických podle středu symetrie.

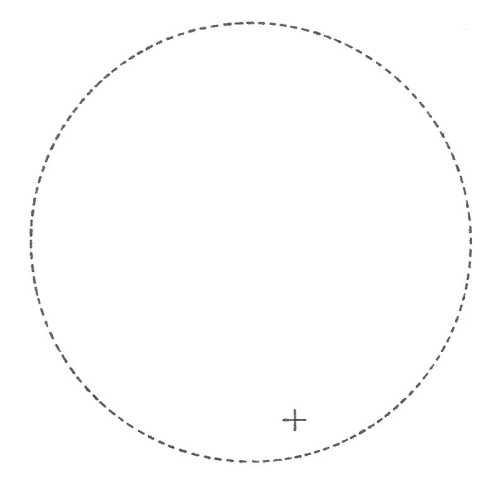
Oddělení triklinicky pediální (1) – není přítomen žádný prvek symetrie a každá plocha tvoří samostatný krystalový tvar – pedion.

Soustava monoklinická

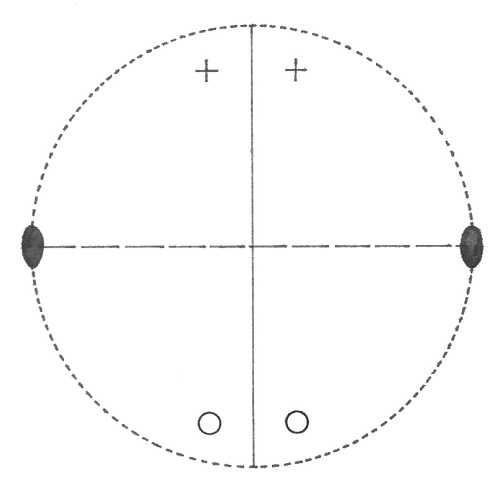
Oddělení monoklinicky prizmatické (2/m) – ve směru osy b je dvojčetná rotační osa symetrie a na ni je kolmá rovina symetrie. Plocha v obecné poloze dá vzniknout čtyřplochému otevřenému krystalovému tvaru – pinakoidu.

Oddělení monoklinicky domatické (m) – přítomna je rovina symetrie kolmá na osu b. Z plochy, která leží v obecné poloze mimo rovinu symetrie, vzniká dvojplochý otevřený tvar – dóma. Plochy rovnoběžné s rovinou symetrie se zobrazují jako pinakoidy, plochy kolmé na rovinu symetrie se stávají pediony.

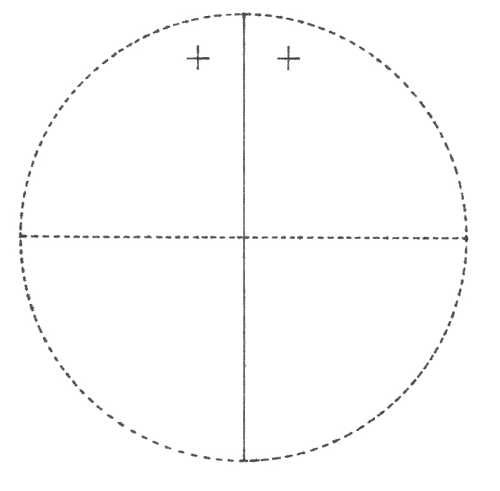
Oddělení monoklinicky sfenoidické (2) – přítomna je dvojčetná osa symetrie ležící v ose b. Z plochy, která neleží na prvku symetrie, vzniká dvojplochý otevřený tvar – sfenoid. Plocha ležící na ose symetrie zůstává pedionem.

Soustava rombická

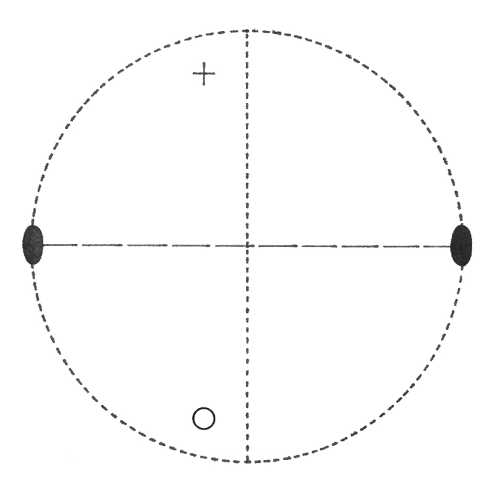
Oddělení rombicky dipyramidální (2/m 2/m 2/m) – v osních rovinách leží roviny symetrie a na každou z nich je kolmá dvojčetná osa symetrie. Kombinace výše uvedených prvků symetrie dává vzniknout i středu symetrie. Plocha v obecné poloze se promítne do osmiplochého uzavřeného tvaru – rombické dipyramidy.

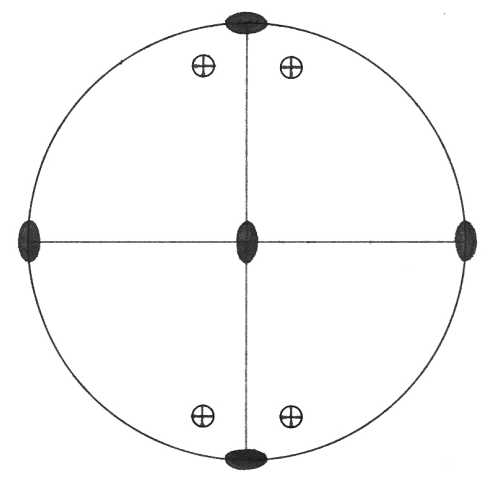
Oddělení rombicky pyramidální (mm2) – dvojčetná osa symetrie ve směru krystalografické osy c tvoří průsečík dvou vzájemně kolmých rovin symetrie. Plocha v obecné poloze dává vzniknout otevřenému čtyřplochému tvaru – rombické pyramidě (zakreslena je pyramida horní).

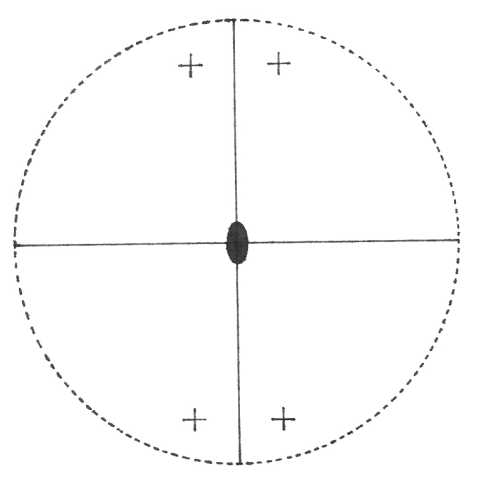
Oddělení rombicky disfenoidické (222) – v osních směrech leží tři navzájem kolmé dvojčetné rotační osy symetrie a z plochy v obecné poloze vznikne uzavřený čtyřplochý tvar – disfenoid (zde zakreslen disfenoid pozitivní).

Soustava tetragonální

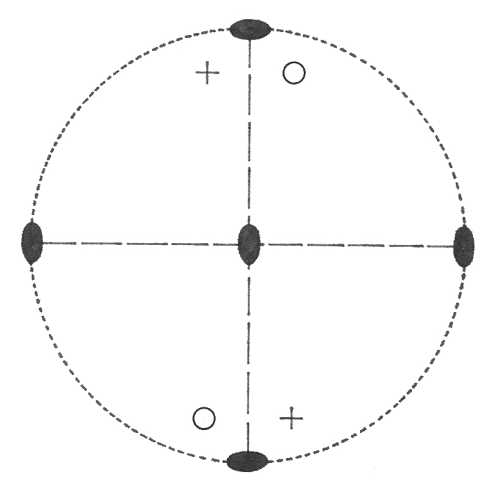
Oddělení ditetragonálně dipyramidální (4/m 2/m 2/m) – s vertikálou je totožná čtyřčetná rotační osa symetrie a na ni je kolmá pasná rovina symetrie. Ve směru pasných os a v meziosních směrech je vždy dvojčetná rotační osa symetrie a na každou kolmá vertikální rovina symetrie, takže čtyři roviny symetrie se protínají ve vertikální čtyřčetné ose symetrie. Přítomen je střed symetrie. Z plochy v obecné poloze vznikne krystalový tvar ditetragonální dipyramida.

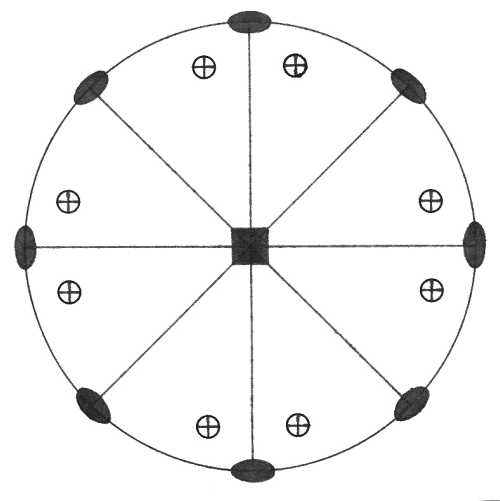
Oddělení ditetragonálně pyramidální (4mm) – ve vertikálním směru osy c leží čtyřčetná rotační osa symetrie, ve které se protínají čtyři vertikální roviny symetrie. Pasná rovina symetrie a v ní ležící dvojčetné rotační osy symetrie chybí, podobně jako střed symetrie. Plocha v obecné poloze se zobrazí jako ditetragonální pyramida (zde varianta horní).

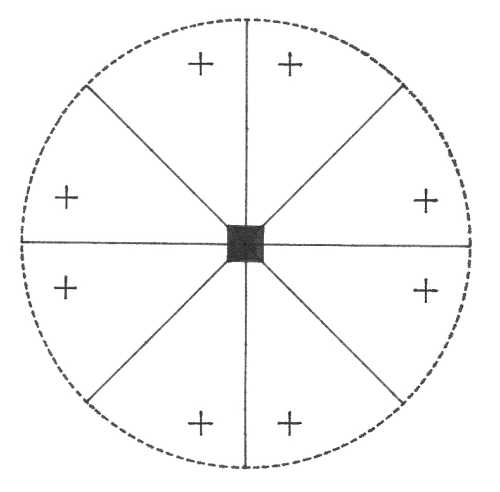
Oddělení tetragonálně skalenoedrické (-42m) – s vertikálou je totožná čtyřčetná inverzní osa symetrie, v osních směrech jsou dvě horizontální dvojčetné rotační osy symetrie a v meziosních směrech jsou dvě vertikální roviny symetrie (protínají se ve vertikále). Plocha v obecné poloze se zobrazí jako tetragonální skalenoedr.

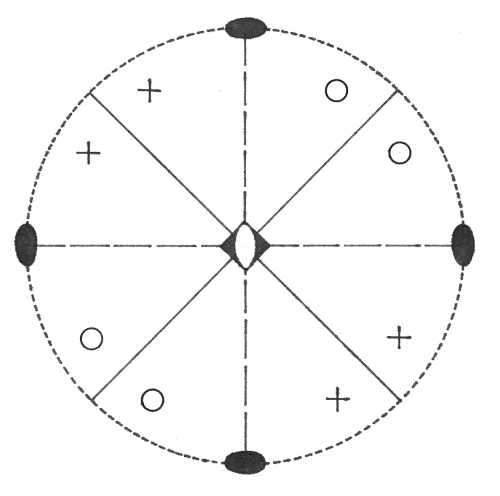
Oddělení tetragonálně dipyramidální (4/m) – přítomna je pouze vertikální čtyřčetná rotační osa symetrie a na ni je kolmá pasná rovina symetrie. Plocha v obecné poloze se zobrazí jako tetragonální tritodipyramida.

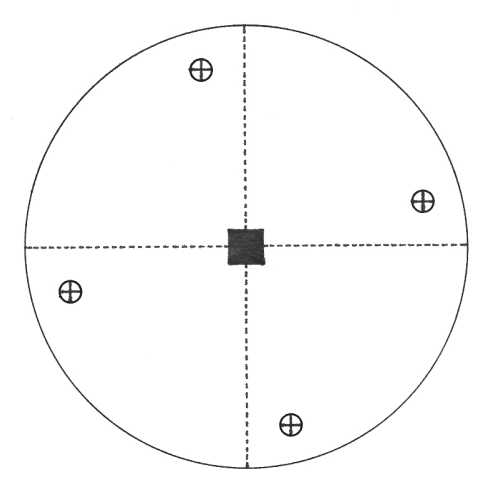
Oddělení tetragonálně trapezoedrické (422) – v pozici vertikály najdeme čtyřčetnou rotační osu symetrie a na ni jsou v osních a meziosních směrech kolmé čtyři dvojčetné rotační osy symetrie. Plocha v obecné poloze se zobrazí jako tetragonální trapezoedr.

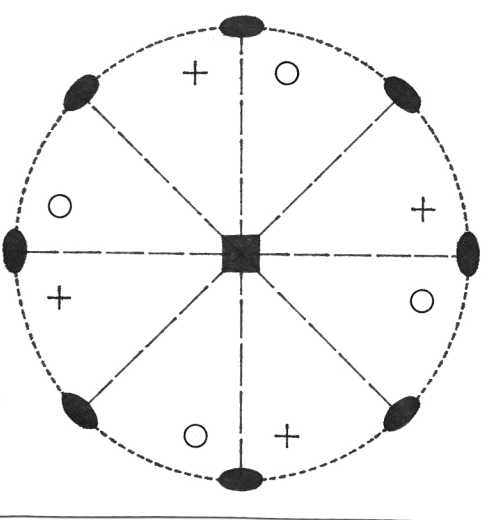
Oddělení tetragonálně disfenoidické (-4) – přítomna je pouze vertikální čtyřčetná inverzní osa symetrie. Plocha v obecné poloze se zobrazí jako čtyřplochý uzavřený krystalový tvar - tetragonální tritodisfenoid.

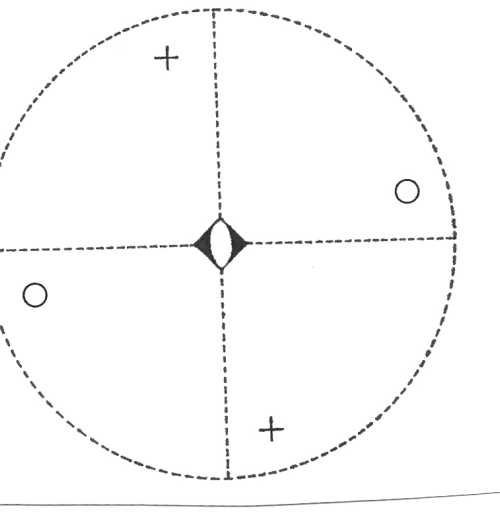
Oddělení tetragonálně pyramidální (4) – přítomna je pouze vertikální čtyřčetná rotační osa symetrie. Plocha v obecné poloze se zobrazí jako čtyřplochý otevřený krystalový tvar - tetragonální tritopyramida.

Soustava hexagonální

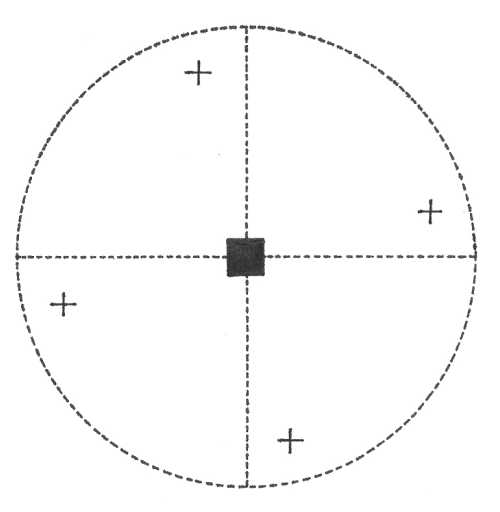
Oddělení dihexagonálně dipyramidální (6/m 2/m 2/m) – vertikále odpovídá šestičetná rotační osa symetrie a na ni je kolmá pasná rovina symetrie. Ve směru pasných os a v meziosních směrech je vždy dvojčetná rotační osa symetrie a na ni kolmé vertikální roviny symetrie, takže šest rovin symetrie se protíná ve vertikální šestičetné ose symetrie. Přítomen je střed symetrie. Plocha v obecné poloze se zobrazí jako 24-plochý uzavřený krystalový tvar - dihexagonlní dipyramida.

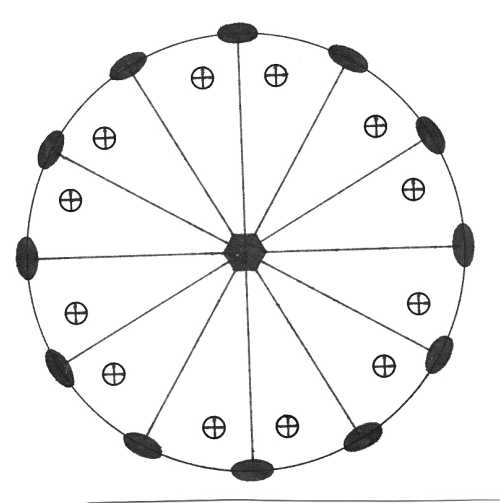
Oddělení dihexagonálně pyramidální (6mm) – ve vertikálním směru osy c je šestičetná rotační osa symetrie, ve které se protíná šest vertikálních rovin symetrie. Pasná rovina symetrie a v ní ležící dvojčetné rotační osy symetrie chybí. Plocha v obecné poloze se zobrazí jako 12-ti plochý otevřený krystalový tvar - -dihexagonální pyramida.

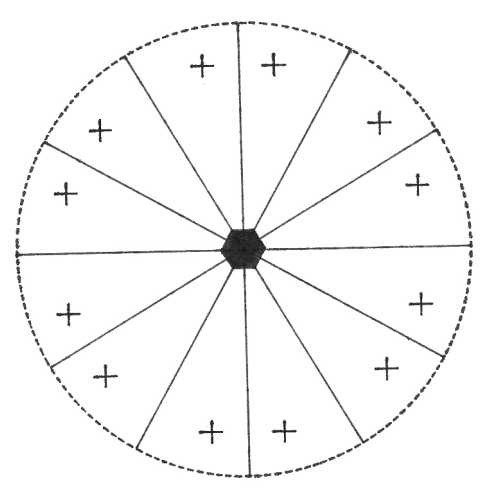
Oddělení hexagonálně dipyramidální (6/m) – přítomna je pouze vertikální šestičetná rotační osa symetrie a na ni je kolmá pasná rovina symetrie. Z plochy v obecné poloze vzniká hexagonální tritodipyramida.

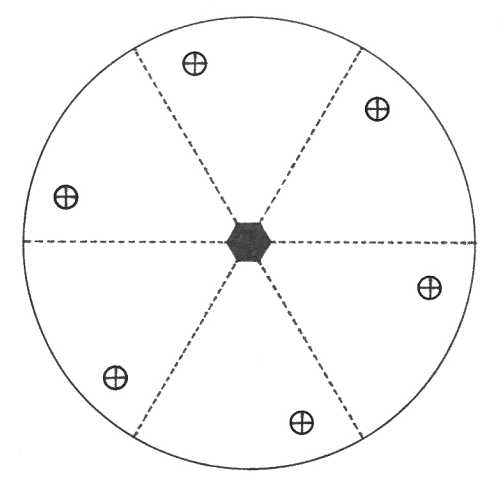
Oddělení hexagonálně trapezoedrické (622) – v pozici vertikály najdeme šestičetnou rotační osu symetrie a na ni je v osních a meziosních směrech kolmých šest dvojčetných rotačních os symetrie. Plocha v obecné poloze se zobrazí jako uzavřený 12-ti plochý tvar - hexagonální trapezoedr.

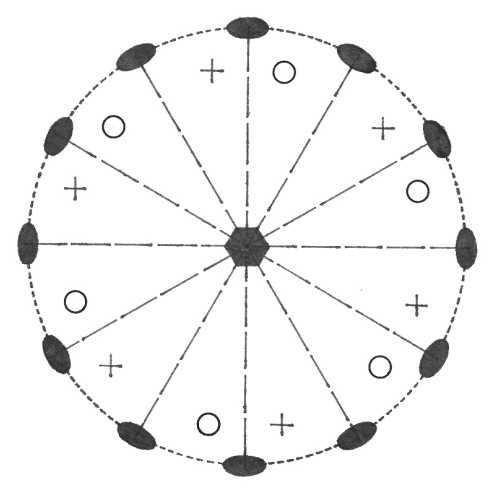
Oddělení hexagonálně pyramidální (6) – přítomna je pouze vertikální šestičetná rotační osa symetrie. Z plochy v obecné poloze vznikne šestiplochý otevřený tvar - hexagonální tritopyramida.

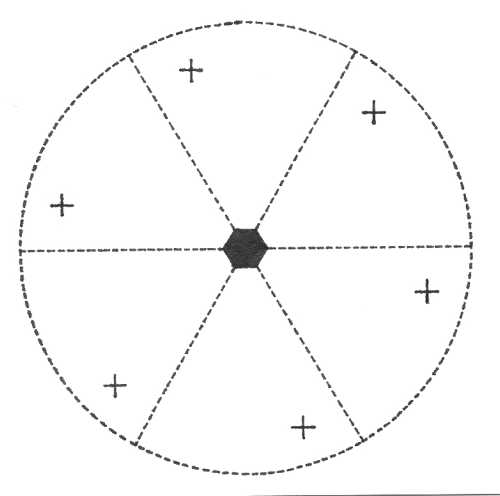
Oddělení ditrigonálně dipyramidální (-6m2) – vertikálu tvoří šestičetná inverzní osa symetrie, kterou můžeme nahradit trojčetnou rotační osou symetrie a na ni kolmou pasnou rovinou symetrie. V pasné rovině leží v meziosním směru tři dvojčetné rotační osy symetrie a tři vertikální roviny symetrie. Obecná plocha umožní vznik dvanáctiplochého uzavřeného krystalového tvaru - ditrigonální dipyramidy.

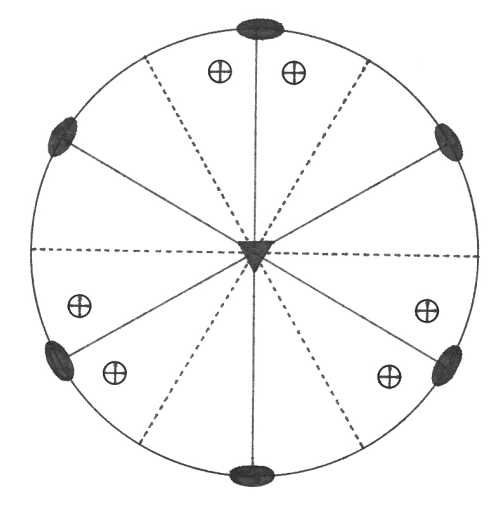
Oddělení trigonálně dipyramidální (-6) – vertikálu tvoří šestičetná inverzní osa symetrie, což je totéž jako vertikální trojčetná rotační osa symetrie a na ni kolmá pasná rovina symetrie. Obecná plocha se zobrazí jako šestiplochý uzavřený tvar - trigonální dipyramida.

Soustava trigonální

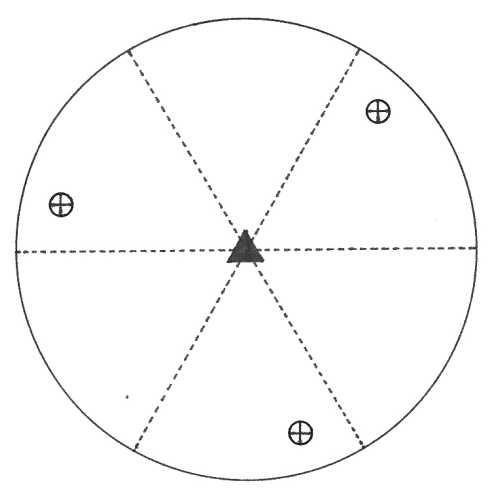
Oddělení ditrigonálně skalenoedrické (-3 2/m) – s vertikálou souhlasí trojčetná inverzní osa symetrie (představuje kombinaci trojčetné rotační osy symetrie a středu symetrie). Ve směru pasných os jsou tři dvojčetné rotační osy symetrie a na ně jsou v meziosním směru kolmé tři vertikální roviny symetrie. Obecným krystalovým tvarem je dvanáctiplochý uzavřený ditrigonální skalenoedr.

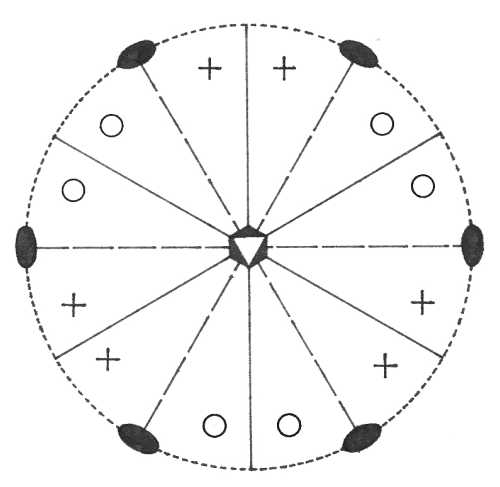
Oddělení ditrigonálně pyramidální (3m) – vertikálu tvoří trojčetná rotační osa symetrie, ve které se protínají tří vertikální roviny symetrie v meziosním směru. Z plochy v obecné poloze vznikne šestiplochý otevřený tvar - ditrigonální pyramida.

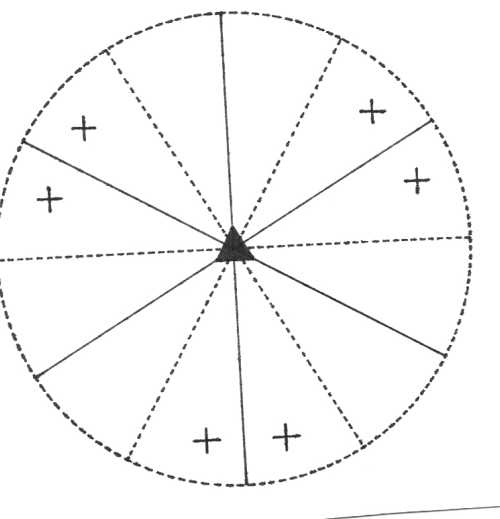
Oddělení trigonálně trapezoedrické (32) – vertikálu tvoří trojčetná rotační osa symetrie, na kterou jsou kolmé tři horizontální dvojčetné rotační osy symetrie v osních směrech. Plocha v obecné poloze se zobrazí jako trigonální trapezoedr.

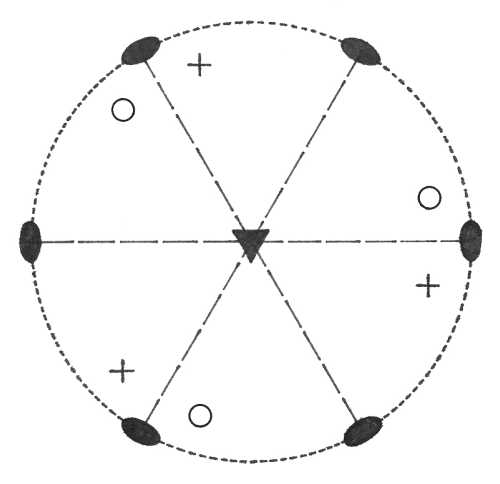
Oddělení trigonálně romboedrické (-3) – přítomna je pouze trojčetná inverzní osa symetrie, která je totéž jako trojčetná rotační osa symetrie v kombinaci se středem symetrie. Plocha v obecné poloze dá vzniknout tritoromboedru.

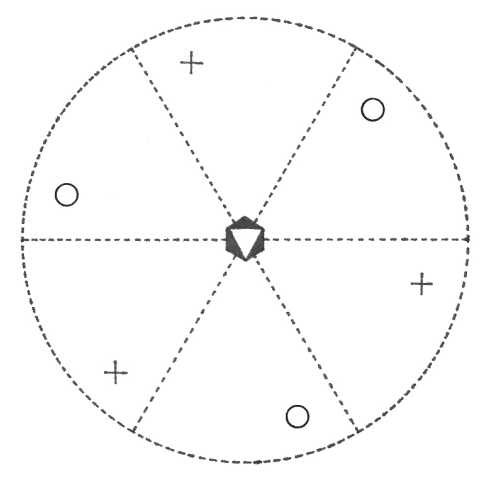
Oddělení trigonálně pyramidální (3) – přítomna je pouze vertikální trojčetná rotační osa symetrie. Obecným tvarem je trigonální tritopyramida.

Soustava kubická

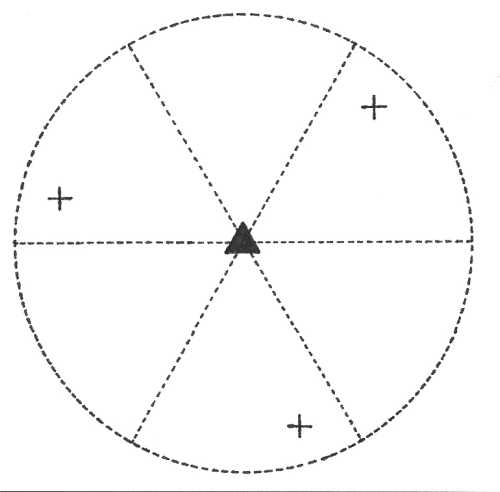
Oddělení hexaoktaedrické (4/m –3 2/m) – ve směru krystalografických os najdeme tří čtyřčetné rotační osy symetrie a na každou z nich je kolmá rovina symetrie. Ve směru tělesové úhlopříčky krychle <111> najdeme čtyři trojčetné inverzní osy symetrie (odpovídají kombinaci trojčetné rotační osy symetrie a středu symetrie). Ve směru stranových úhlopříček krychle <110> leží celkem šest dvojčetných rotačních os symetrie a na každou je kolmá rovina symetrie. Obecným krystalovým tvarem je osmačtyřicetistěn - hexaoktaedr.

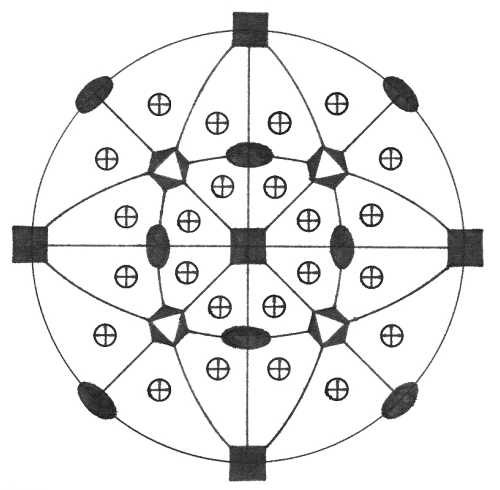
Oddělení hexatetraedrické (-43m) – ve směru krystalografických os jsou přítomny tři čtyřčetné inverzní osy symetrie, ve směru tělesových úhlopříček krychle <111> leží čtyři trojčetné rotační osy symetrie a kolmo na směr <110> leží šest rovin symetrie. Obecným krystalovým tvarem je 24-plochý uzavřený hexatetraedr.

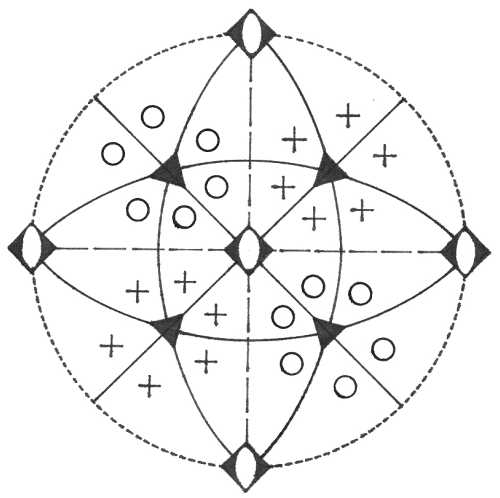
Oddělení didokaedrické (2/m-3) – v osních směrech najdeme tři dvojčetné rotační osy symetrie a na ně kolmé roviny symetrie, směr <111> je vyhrazen pro čtyři trojčetné inverzní osy symetrie. Plocha v obecné poloze se zobrazí jako 24-plochý krystalový uzavřený tvar - didokaedr.

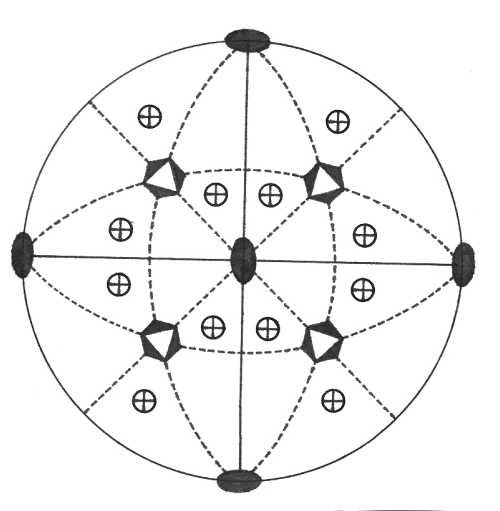
Oddělení pentagon trioktaedrické (432) – v osních směrech jsou tři čtyřčetné rotační osy symetrie, ve směru <111> jsou čtyři trojčetné rotační osy symetrie a ve směru <110> je celkem šest dvojčetných rotačních os symetrie. Plocha v obecné poloze se zobrazí jako uzavřený krystalový tvar - pentagon trioktaedr.

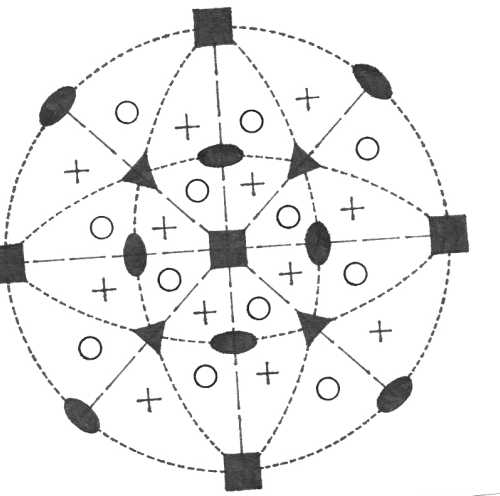
Oddělení pentagon tritetraedrické (23) – v osních směrech jsou tři dvojčetné rotační osy symetrie, ve směrech <111> jsou čtyři trojčetné rotační osy symetrie. Plocha v obecné poloze umožní vzniku uzavřeného krystalového tvaru pentagon tritetraedru.