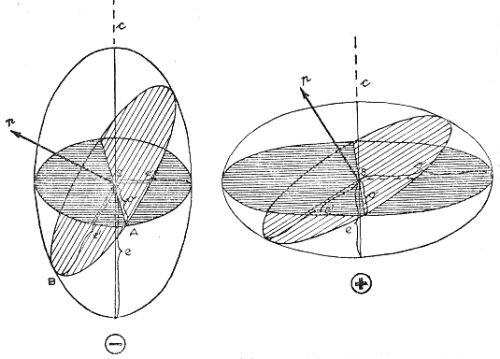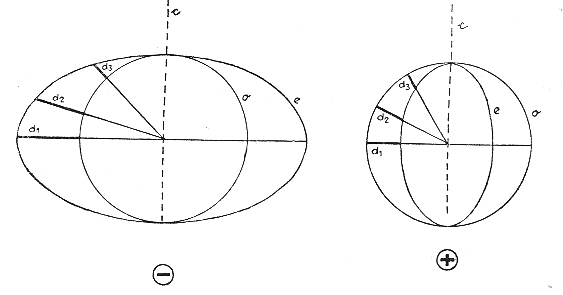
Fresnelův elipsoid
Grafické znázornění pohybu světelných paprsků v jednoosých minerálech je možné provést pomocí vlnoploch. Vyházejí-li ze středu krystalu paprsky řádné a mimořádné všemi směry, tak v daný časový okamžik budou čela vln řádných paprsků tvořit kulovou plochu, protože se paprsek řádný šíří v krystalu ve všech směrech stejnou rychlostí. Čela všech paprsků mimořádných budou tvořit povrch rotačního elipsoidu, protože v různých směrech se paprsky mimořádné šíří různou rychlostí. Plošný řez takovou situací je na obrázku. Vertikálu (směr osy z) tvoří optická osa a největší rozdíl (d) mezi paprskem řádným (o) a mimořádným (e) je ve směru kolmém na optickou osu. Čím více se přibližuje směr paprsků k optické ose, tím menší je rozdíl mezi rychlostmi obou paprsků, až ve směru optické osy se rychlosti vyrovnají (nedochází k dvojlomu). Rotační elipsoid paprsku mimořádného je kružnici paprsku řádného vepsán nebo opsán v závislosti na optickém charakteru látky.

Pro znázornění vztahu rychlosti paprsku řádného a mimořádného se v reálných krystalech používá Fresnelova elipsoidu. U jednoosých minerálů má tvar rotačního elipsoidu, kdy svislá osa charakterizuje rychlost paprsku mimořádného a vodorovná paprsku řádného. Z diagramu můžeme odvodit rychlost obou paprsků v závislosti na směru (vektor p), v jakém dopadl původní světelný svazek na krystal.