Úhel
optických os je úhel, který mezi sebou svírají optické osy dvojosého
minerálu. V tabulkách se vždy uvádí úhel, který půlí ostrá středná,
tedy úhel do 90°. Jeho hodnota může být dobrým diagnostickým znakem, ale
často jeho velikost kolísá s chemickým složením nebo je závislá na
tlakovém postižení. K jeho měření se používá konometr nebo se měří
přímo z konoskopického obrázku v polarizačním mikroskopu.
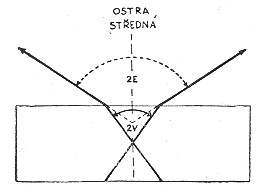
Pro přesná měření se používá Fjodorovova univerzálního stolku. Tato metoda je ale metodicky poměrně náročná, a proto je v některých případech snadnější aplikovat stanovení úhlu 2V pomocí škály mikrometrického okuláru. Měříme vzdálenost vrcholů ramen hyperbol (výchozů optických os) v diagonální poloze. Z této vzdálenosti (2D) lze za určitých předpokladů vypočítat úhel 2V. Jelikož v mikroskopu pozorujeme zdánlivý úhel optických os (2E), který je větší než skutečný, tak i vzdálenost 2D neodpovídá skutečné vzdálenosti výchozů optických os (obrázek podle Hejtman a Konta, 1959). Důvodem je lom od kolmice při přechodu světelných paprsků z látky do vzduchu.

Ze změřené vzdálenosti D musíme vypočítat zdánlivý úhel E za pomoci Mallardovy konstanty. Tu stanovíme pomocí látky, pro kterou byl konometrem přesně stanoven zdánlivý úhel 2E (např. bazální lupínek muskovitu). Stanovení je třeba provést několikrát, aby hodnota konstanty byla přesná – pro daný mikroskop je pak platná jednou provždy. Výpočet je proveden podle vzorce:
KM
= D / sin E.
U studovaného minerálu měříme také vzdálenost 2D a podle vzorce můžeme při znalosti Mallardovy konstanty vypočítat sin E. K výpočtu skutečného úhlu V, potřebujeme znát ještě index lomu b:
sin
V = sin E / b